首先,我们将范围缩小到一个端到端的OFDM收发机物理层。
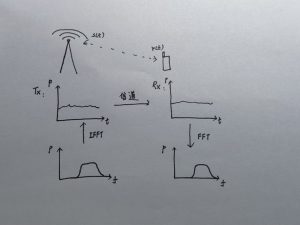
可以看到,我们的数据是放在频域上的,经过IFFT以后,转化为时域信号,通过信道,到达接收机,然后再经过FFT转化为频域信号,再提取出我们想要的数据。
这里解释一个问题,我们为什么要在频域上放数据,而不是在时域上直接放。首先,我们希望我们的数据占用的是一段频带,这样不同用户通过滤波器可以提出自己想要的数据。其次,低频的干扰比较多,我们需要将数据搬移到高频去,避开低频的干扰。
这是大体的流程,但是我们细化到里面去看,真实的收发机内部处理的都是离散的数字信号,我们上图是忽略了DA和AD以及相位谱的,它实际是什么情况呢,我们以QPSK为例,举个例子。
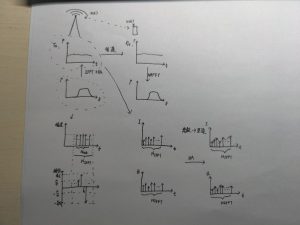
其中Nsub指的是子载波的个数,Nfft指的是FFT点数。
注意一个公式:采样频率fs=Nfft*子载波间隔∆f。
这个公式,我们确定了2个,另一个就被确定了,而且它对收发端都是成立的。那么说明:我们将数据做IFFT变换,将IFFT后的2*Nfft(I,Q分开看)个值按照fs的速率用两路DA发出去,接收端用采样频率fs采样,分IQ两路,再做Nfft点的FFT变换,就相当于在频域做了以∆f为间隔的频域采样,能得到我们之前放的数据!
上面是理想情况,我的信号完全不失真,接收端收的和你发的完全一样,而且我知道你什么时候到我这里。真实情况显然不是这样,我们想想会发生什么事情。(括号里是对应的解决手段)
1.接收端不知道你这个符号什么时候到(时间同步)。
2.由于多普勒效应,时域信号会被拉长或压短;由于发送端和接收端晶振频率的误差,收发端的采样频率并不相等。这两种情况其实都可以归结成接收端fs不是理想的情况(因为时域信号变长变短,换个角度看也可以是采样频率降低或升高),那我们回到这个公式:采样频率fs=Nfft*子载波间隔∆f,说明我们的频域采样的∆f不是理想的。(频率估计和补偿)
3.由于传播损耗、雨衰、多径衰减等,接收端的信号会发生幅值和相位的变化。(信道估计)
关于时间同步的问题。
时间同步是什么情况呢,我接收端不知道你信号什么时候到我这里,我只能一直采数据,要想找到帧头,有两个办法:
- 基于参考信号的:我在帧头发一个特定的时间序列,你用已知的这段序列和我做相关,找到峰值就是这个符号头。
- 基于CP的:我知道你发的序列有个特性,每隔L+N个采样点,前L个采样点和N点以后的L个采样点是一样的,我就拿这前面L个采样点去和后面L个采样点做相关,找到峰值就是符号头。为了更准确,我做多符号合并的,多找几组符号一起做相关。
关于频率估计和补偿的问题。
首先确定一点,频率同步是在时间同步之后做的。频率同步分为小数倍频偏估计和补偿、整数倍频偏估计和补偿这两块。先做小数倍,再做整数倍;小数倍是在时域做的,整数倍是在频域做的。
小数倍:将偏移的点移回到频域采样点上,但是可能会错位,他的纠正范围是±0.5个子载波间隔。
整数倍:类似于时间同步,把点放到正确的位置上,纠正整数个子载波间隔。
关于信道估计的问题。
信号过信道,然后到达接收端,我们知道信号会发生变化,那么怎么去描述这种变化呢。我们假定这个变化是连续的,什么意思呢,就是说,假如我发送端发的是连续函数,那么不考虑突发干扰,你接收端收到的应该也是一个连续函数。
那么连续函数的一个关键特征是什么,它连续,我假设它是h(t,f),假如我知道了h(t-∆t)和h(t+∆t),那么我就能估计出h(t),这里的∆不是微分的极限,所以只能估计。
好,我们以上面为前提,来看这个图
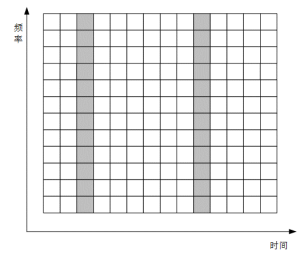
灰色放的是导频,白色是数据,我知道灰色导频的地方发生了什么变化,用这种变化去估计出白色数据处的变化,再做个逆变换,就得到了变化前的数据值。
